MMATHS, Part 3: AfterMMATHS

Well, it’s been a few months since the competition, which has given me ample time to really reflect on what happened.

As my MMATHS compatriot Andrew would say, the competition was a suboptimal play. Now, does this necessarily mean it went poorly? Absolutely not; in fact, I thought it went about as well as it could have. However, hindsight is 20/20, and there’s a very large number of things I would have changed, had I the chance. Let’s go in order of things I had the most influence over.

1. A rewrite of Problem 12. Nobody solved the problem I wrote. While I’m glad that I was able to create a challenging problem, part of the challenge unintentionally came from the relatively large number of calculations needed to solve the problem. As a reminder, here’s the problem statement:

   

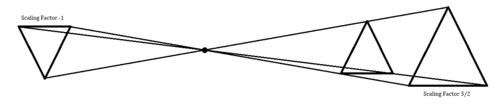
   The answer to this problem is . The general idea of the solution is to notice a few nice homotheties— transformations of space that are scalings centered at some point. These transformations can be described with the point that serves as the center and the factor by which everything is scaled. In this particular problem, there is a homothety centered at the center of the tetrahedron that sends ABC to XYZ with scaling factor -5/3. What does a negative scaling factor mean, you may ask? It simply means that shapes are inverted:

   

   From there, the next logical leap that has to be made is figuring out the general shape of the polyhedron and the idea of “completing the prism.” This is very hard to imagine, but I’m going try and explain it anyway. After thinking about the diagram, it is key to notice that the polyhedron is of the shape of a triangular antiprism (or more precisely, something close to but not quite it; the bases are similar, but not congruent, so it doesn’t exactly fit the description, but I couldn’t find a term that described this shape exactly):

   

   

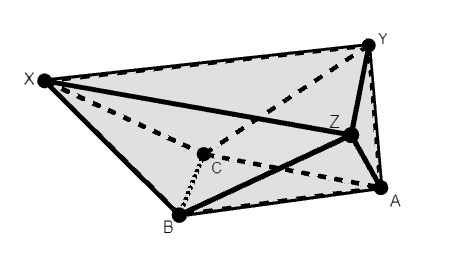
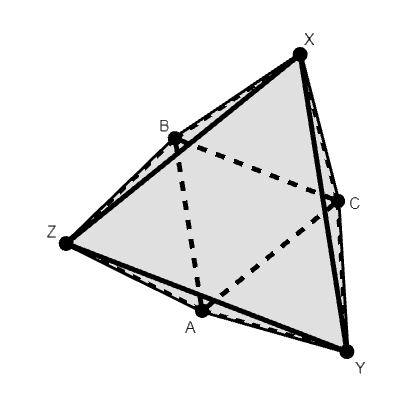
   Note how each vertex has a bit of “overhang” with respect to the face on the opposite side of the object: if you drew a perpendicular from each vertex to the plane containing the opposite face, it would not land inside the face.

   

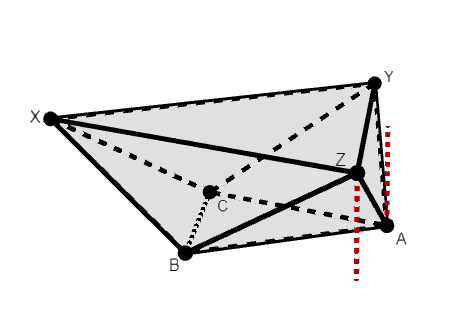
   So, what if we fill in this overhang for all of the vertices? Then, we would have congruent hexagons at both the bottom and the top of the polyhedron, with edges perpendicular to the bases connecting corresponding vertices— a prism!

   

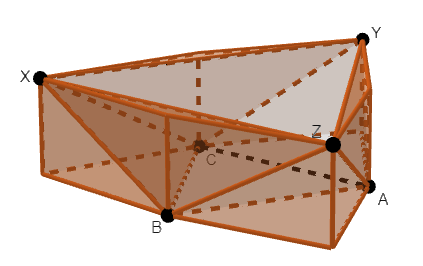
   So, we can find the volume by finding the volume of this prism and subtracting out the overhang we filled in, which contains six pyramids, and we’re done.

   Anyway, as much as I enjoy this problem and enjoy the solution to the problem, I realize now that there’s a crucial flaw with it— it simply requires too many calculations. Participants had 75 minutes to do 12 problems, which averages out to be just over 6 minutes per problem. This just simply isn’t enough time to do all these steps I presented! Instead, I should have figured out a way to “cut off” the problem somewhere to reduce the calculations or requested that it be moved to the tiebreaker round.

2. Time Management. I’m actually pretty responsible for this now, because I’m now one of the new problem writing heads for future competitions! My new plan is to try and get started writing problems earlier, which has been successful for the time being. For MMATHS, a very large portion of the problems was written in the week leading up to the competition. In addition to a lot of stress, a few mistakes made it through to the contest, which was unfortunate. It’s always a bit frustrating to see a small error slip through and make it to the final tests; not only do we have to actually correct the error, we have to also consider whether or not to accept previously submitted answers, We’ll have to see a few months from now, though.

3. More preparation for contest day. Although delays are rather typical for math competitions, at least for the ones I frequented as a high schooler, there were definitely a few things that would have gone better had I the time to rehearse. One example is the problem discussion, which, granted, was never planned to happen until the incident surrounding our guest speaker happened; I had to explain my solution to Problem 12 on the fly while trying to not take too much time to dabble in the details, which didn’t work out perfectly.

4. Online Social Events. For me, the social aspect of math competitions was a key reason why I participated in so many of them; getting to converse and participate in fun events with so many people with the same interests as I was definitely some of the highlights of high school! Unfortunately, this is really hard to pull off for a virtual event; talking to people over zoom doesn’t really carry the same vibes as talking with them in person.

And that’s all I can think of at the moment! I’m pretty confident that things’ll work out for Girls in Math on 2/26!

Note: I forgot to include the answer to the geometry problem in the previous post. It is .