
(Warning: This will be a very math-heavy post.)
I hope it’s clear at this point that I enjoy math. There’s just something about the ability to construct such beautiful, complex ideas from basic building blocks that fascinates me every time I explore it, whether in math class or on my own.
Recently the Yale Math Competition Club put on MMATHS - the Math Majors of America Tournament for High Schools. MMATHS is a contest run by us Yalies for high schoolers (and occasionally some prodigious middle schoolers) across the globe! Because of the ever-present pandemic, like last year, the competition this year is being held online, so things operate a little differently as compared to previous years. I helped write problems and helped operate the competition last Saturday. Things went pretty well!
The members of the Math Competition Club met weekly to write problems (and very often the last week before the competition because of procrastination), throwing ideas around and test-solving problems we wrote and complaining about being unable to come up with new ideas. It was a great time; discussing math and panicking over the deadline builds a very strong sense of camaraderie. We also had occasional logistics meetings discussing how to actually run the competition, how budgeting works each year, etc.

Two problem writers hard at work, at a table in the Silliman Buttery. They probably won’t like that I described them that way, which is precisely why I chose to do so. Hehe.

My workplace at a MMATHS logistics meeting. We got food from Steamed. It was tasty. Please excuse my chopstick etiquette.
Although I did do some logistics work, almost all of my time helping run MMATHS was related to problem writing. So, how do you write a competition math problem? Although I’m admittedly not extraordinarily qualified to talk about problem writing, I’ll go through the process of how I came up with a problem in the past, one that I wrote for my all-state math team.

There’s a lot to unpack here, so let’s start from the very beginning. I was thinking about Lagrange Multipliers, or at least something related to them: tangents. When you have a one-dimensional (smooth) function, you can see where a horizontal line is tangent to the function to find a local maximum or minimum of that function:
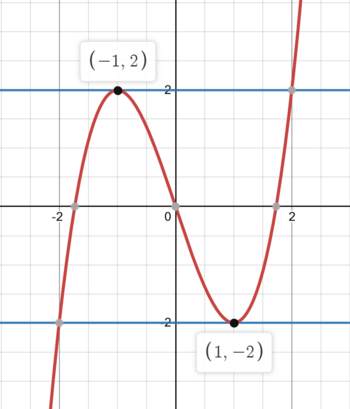
But why stop there? If we rotate the line and move it around, it can be described by the equation , and by fixing
and
, we fix the direction of the line; adjusting
simply shifts the line away and towards the origin. Additionally, large values of
means the line is farther away from the origin, which means that when the line is tangent to our function, there is a local minimum or maximum for
.
Lagrange Multipliers are essentially an extension of this idea to multiple dimensions. The problem is that this is technically a calculus-level subject, which means it is beyond the scope of high school math and therefore beyond the scope of a high school math contest. However, if we restrict things to three dimensions or fewer, it’s easy to make a geometric argument for why a tangent line or plane would result in a local maximum or minimum, as I have just done.
Points of tangency are rather straightforward to find if it’s between a sphere and a plane; the segment drawn from the center of the sphere to the point of tangency is perpendicular to the plane of tangency. Additionally, the lines that are perpendicular to a plane with equation are parallel to the line connecting
to
. Since the line segment between these two points has length
, the planes that are tangent to a sphere with radius
, centered at the point
, are tangent at the points
.
These facts are a bit tedious to prove rigorously, so, unfortunately, you’re going to have to take my word for it. Or take a math class where the teacher’s actually good at explaining these things.
However, I can’t just ask people to optimize some boring polynomial given some boring linear constraint. It has to be made more interesting. How can we obfuscate this a little so that it’s not a one-step process to solving the problem? Well, this took a bit more messing around with math.
A few weeks before I wrote this problem, I was writing more problems for my high school math team. One of the topics for the upcoming MN State Math League meet was logarithms, and so I wanted to come up with some interesting problems involving those. An interesting property I found was that , and since equations for spheres are of the form
with a simple substitution and a couple of change of base formulas, we can get to the problem statement. I’m not going to go through the details, because I want you to have the chance to solve the problem. So, the answer will be posted in the next part of my MMATHS posts. Have fun!
So, that’s how you write a problem. Or, at least, one way I once wrote a problem. Of course, there are many, many ways to write good problems; one could just as easily start from a desired result and work backwards, or take inspiration from somebody else’s problem, or mess around with a compass and ruler for a few hours, or so on and so forth. It all depends on what inspiration strikes at the moment, or if there’s pressure forcing you to do this dozens of times within a week. It’s been a wonderful time doing this for the last few weeks, and I foresee myself having fun writing problems for years to come.
And that’s all for problem writing! Next time, I’ll be going over how the contest actually went, a problem I wrote for the competition, and some overall thoughts.

















